Cómo calcular la producción, el precio y los beneficios de las ecuaciones de monopolio.
Pregunta de los lectores: Un monopolista opera bajo una tecnología de producción que permite la producción de cualquier nivel de producción a un costo promedio constante de $ 5 por unidad. Este monopolista vende en dos mercados distintos cuyas curvas de demanda son: P1 = 55-Q1 (para el mercado uno) y Q2 = 70 – 2P2 (para el mercado 2). Si este monopolista opera para maximizar la ganancia total, entonces calcule:
(i) Producción total;
(ii) La cantidad vendida en cada mercado;
(iii) El precio cobrado en cada mercado;
(iv) La ganancia total del monopolista.
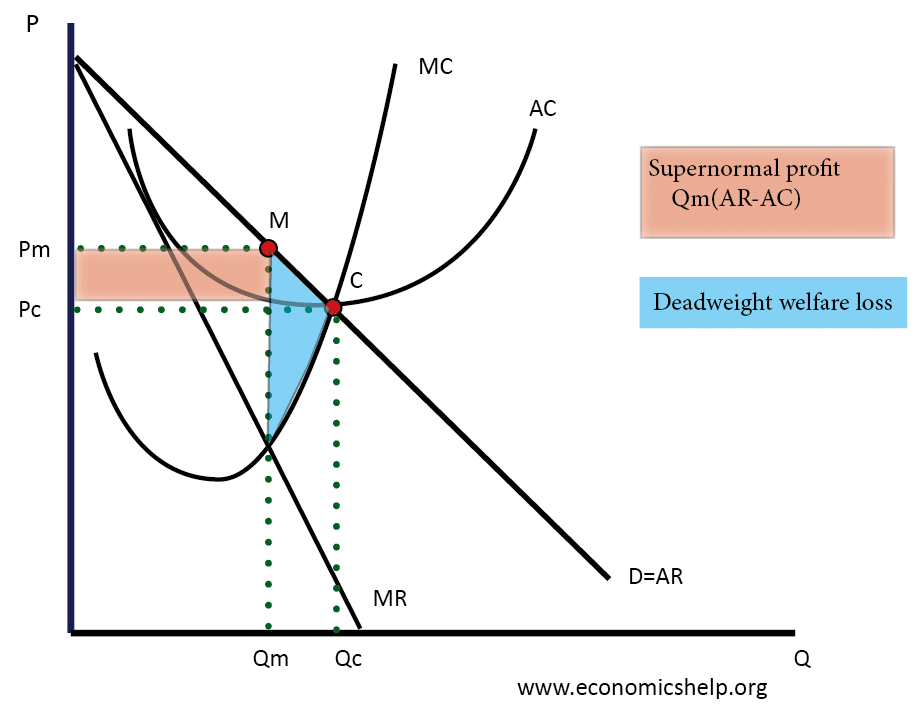
La curva de demanda es igual a la curva de ingresos promedio.
Necesitamos averiguar la curva de ingresos marginales
La curva de ingresos marginales es dos veces más empinada.
- Si QD = 55 – P1 (AR).
- P = 55 – Q
- MR = 55 -2Q1
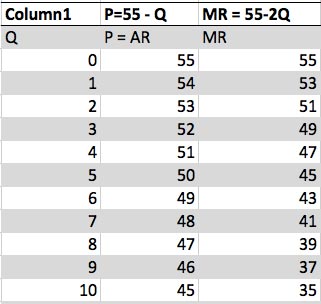
El siguiente paso es trabajar en la maximización de beneficios.
Maximización de beneficios para un monopolista
- La maximización de beneficios ocurre donde MR = MC
- MC = $ 5 (un costo promedio constante significa MC = AC)
- MR = 55 -2Q
Por lo tanto,
- 5 = 55 – 2Q
- 2Q = 50
- Q = 25
- P = 55 – Q
- P = 30
Ejemplo usando diagrama
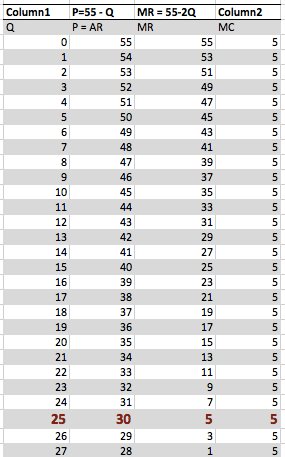
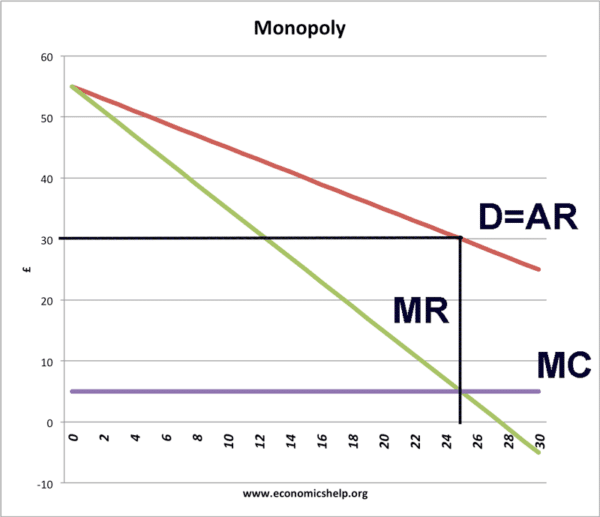
Maximización de beneficios en Q = 25. Precio = 30
Para calcular las ganancias de un monopolio
Beneficio = Ingresos totales – Costo total
Ingresos totales = 25 * 30 = 750
Costo total = 5 * 25 = 125
- Por lo tanto, la ganancia total para esta sección es = 625 (asumiendo que no hay un costo fijo)
Relacionado
- Diagrama de monopolio
- Ecuaciones de oferta y demanda